Category: Paper Announcement
-
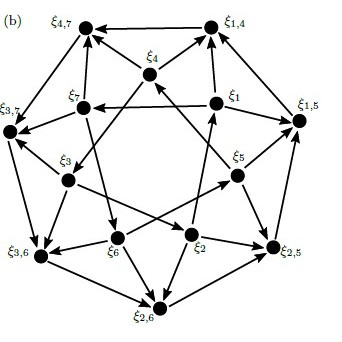
Stability of heteroclinic cycles in rings of coupled oscillators
Posted on
by
Complex networks of interconnected physical systems arise in many areas of mathematics, science and engineering. Many such systems exhibit heteroclinic cycles – dynamical trajectories that show a roughly periodic behaviour, with non-convergent time averages.
-
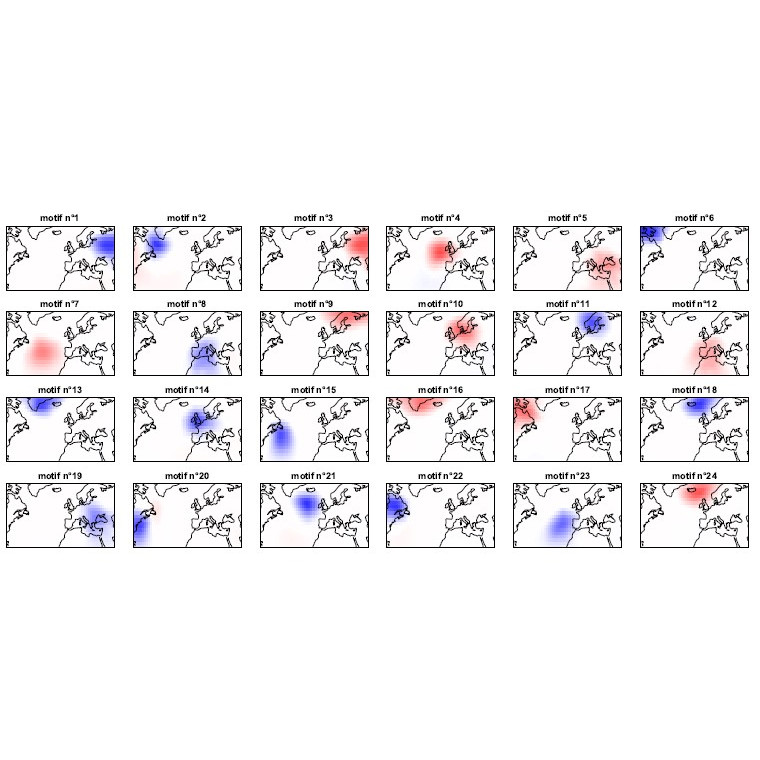
Learning a weather dictionary of atmospheric patterns using Latent Dirichlet Allocation
Posted on
by
The mid-latitude atmospheric circulation is challenging to describe due to the turbulent and chaotic nature of the underlying flow, driven by the unstable dynamics of the jet stream. In general, the phase space of such turbulent geophysical flows appears to be large. […]
-
Metrics and Mechanisms: Measuring the Unmeasurable in the Science of Science
Posted on
by
How does science work? What are its core mechanisms? In recent decades, research has increasingly explored such questions using a variety of quantitative metrics which can be easily calculated from publications. But some of these can be deceiving.
-
Ranking earthquake forecasts using proper scoring rules: Binary events in a low probability environment
Posted on
by
Probabilistic earthquake forecasts can be used to estimate the chance of future earthquake hazards, or to model important risk quantities including the number of fatalities, damaged elements of infrastructure or economic losses. The Collaboratory for the Study of Earthquake Predictability (CSEP)
-
Measuring Unfair Inequality: Reconciling Equality of Opportunity and Freedom from Poverty
Posted on
by
Over the past few decades, rising income inequality has spurred debates around the world. While many call for policies to help redistribute wealth and counter inequality, others argue that inequality is actually necessary to both motivate and reward hard work and economic […]
-
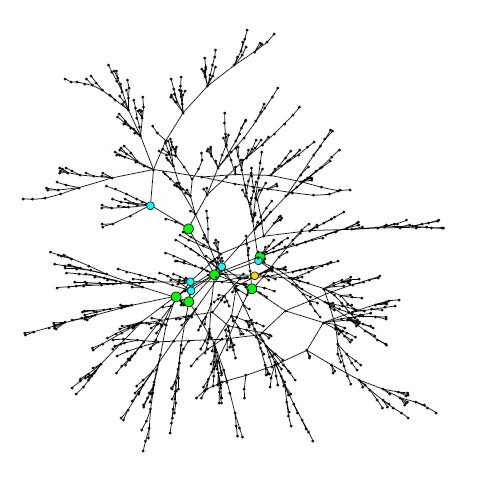
Inference on the History of a Randomly Growing Tree
Posted on
by
The skeletal outlines of many natural processes resemble growing tree-like networks. Examples include the movement of a disease through a human community, news or rumours through social media or a computer virus through a web of connected computers. The elements in these […]
-
London traffic, climate lawsuits and the paradoxical nature of science
Posted on
by
Here are some links to several recent articles by LML External Fellow Mark Buchanan London’s traffic problems won’t be solved by a new driving tax Bloomberg Opinion 22 February, 2022 How do you get to work in the morning? If you live […]
-
Epidemic oscillations induced by social network control: the discontinuous case
Posted on
by
Since the early days of control theory, engineers have understood that feedback can give rise to spontaneous and sustained oscillations. Examples abound in engineering systems such as thermostats and steering devices, as well as in natural and biological systems – for example, […]
-
The Long Run Evolution of Absolute Intergenerational Mobility
Posted on
by
In the mid-20th century, many developed economies experienced several generations of high prosperity, with children generally earning higher incomes than their parents had at the same age. In economics, this is technically known as increasing absolute intergenerational mobility. For the United States, […]
-
Choice history effects in mice and humans improve reward harvesting efficiency
Posted on
by
In foraging for food and other resources, animals have to make repeated choices about where best to search. Experimental studies of such decisions typically work with the simplifying assumption that animals’ past decisions should have no impact on the distribution of actual […]